Description of Gaussian Naive Bayes Classifier

Naive Bayes classifiers are simple supervised machine learning algorithms used for classification tasks. They are called “naive” because they assume that the features are independent of each other, which may not always be true in real-world scenarios. The Gaussian Naive Bayes classifier is a type of Naive Bayes classifier that works with continuous data. Naive Bayes classifiers have been shown to be very effective, even in cases where the the features aren’t independent. They can also be trained even with small datasets and are very fast once trained.

Main Idea: The main idea behind the Naive Bayes classifier is to use Bayes’ Theorem to classify data based on the probabilities of different classes given the features of the data. Bayes’ Theorem says that we can tell how likely something is to happen, based on what we already know about something else that has already happened.

Gaussian Naive Bayes: The Gaussian Naive Bayes classifier is used for data that has a continuous distribution and does not have defined maximum and minimum values. It assumes that the data is distributed according to a Gaussian (or normal) distribution. In a Gaussian distribution the data looks like a bell curve if it is plotted. This assumption lets us use the Gaussian probability density function to calculate the likelihood of the data. Below are the steps needed to train a classifier and then use to to classify a sample record.

Steps to Calculate Probabilities (the hard way):

1. Calculate the Averages (Means):
   • For each feature in the training data, calculate the mean (average) value.
   • To calculate the mean the sum of the values are divided by the number of values.
   • 
2. Calculate the Square of the Difference:
   • For each feature in the training data, calculate the square of the difference between each feature value and the mean of that feature.
   • To calculate the square of the difference we subtract the mean from a value and square the result.
   • 
3. Sum the Square of the Difference:
   • Sum the squared differences for each feature across all data points.
   • Calculating this is easy, we just add up all the squared differences for each feature.
   • 
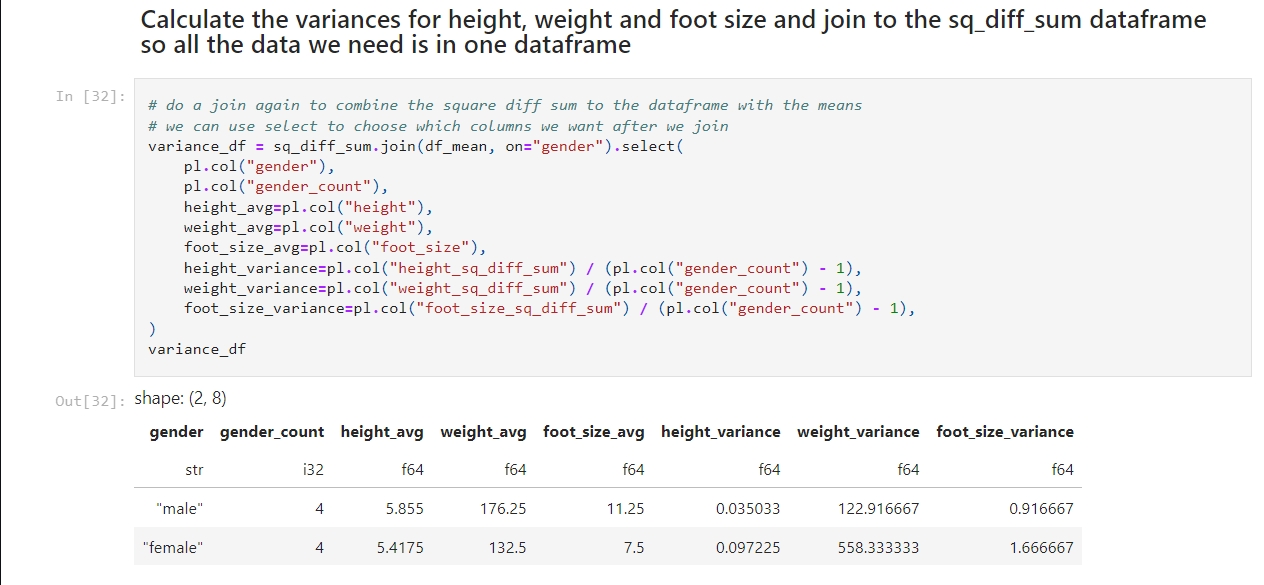
4. Calculate the Variance:
   • Calculate the variance for each feature using the sum of the squared differences.
   • We calculate the variance by dividing the sum of the squares of the differences by the number of values minus 1.
   • 
5. Calculate the Probability Distribution:
   • Use the Gaussian probability density function to calculate the probability distribution for each feature.
   • The formula for this is complicated! It goes like this:
     • First take: 1 divided by the square root of 2 times pi times the variance.
     • Multiply that by e to the power of -1 times the square of the value to test minus the mean of the value divided by 2 times the variance.
   • 
6. Calculate the Posterior Numerators:
   • Calculate the posterior numerator for each class by multiplying the prior probability of the class with the probability distributions of each feature given the class.
   • 
7. Classify the sample data:
   • The higher result from #6 is the result.
   • 

I created a Jupyter notebook that performs these calculations based on this example I found on Wikipedia. Here is my notebook on GitHub. If you follow the instructions in my previous post you can run this notebook for yourself.

– William

References

1. Wikipedia contributors. (2025, February 17). Naive Bayes classifier. In Wikipedia, The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/Naive_Bayes_classifier
2. Wikipedia contributors. (2025, February 17). Variance: Population variance and sample variance. In Wikipedia, The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/Variance#Population_variance_and_sample_variance
3. Wikipedia contributors. (2025, February 17). Probability distribution. In Wikipedia, The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/Probability_distribution