William's Data Science Blog

Category: Kaggle

  • First Experiment with SHAP Visualizations

    First Experiment with SHAP Visualizations

    William's Data Science Blog

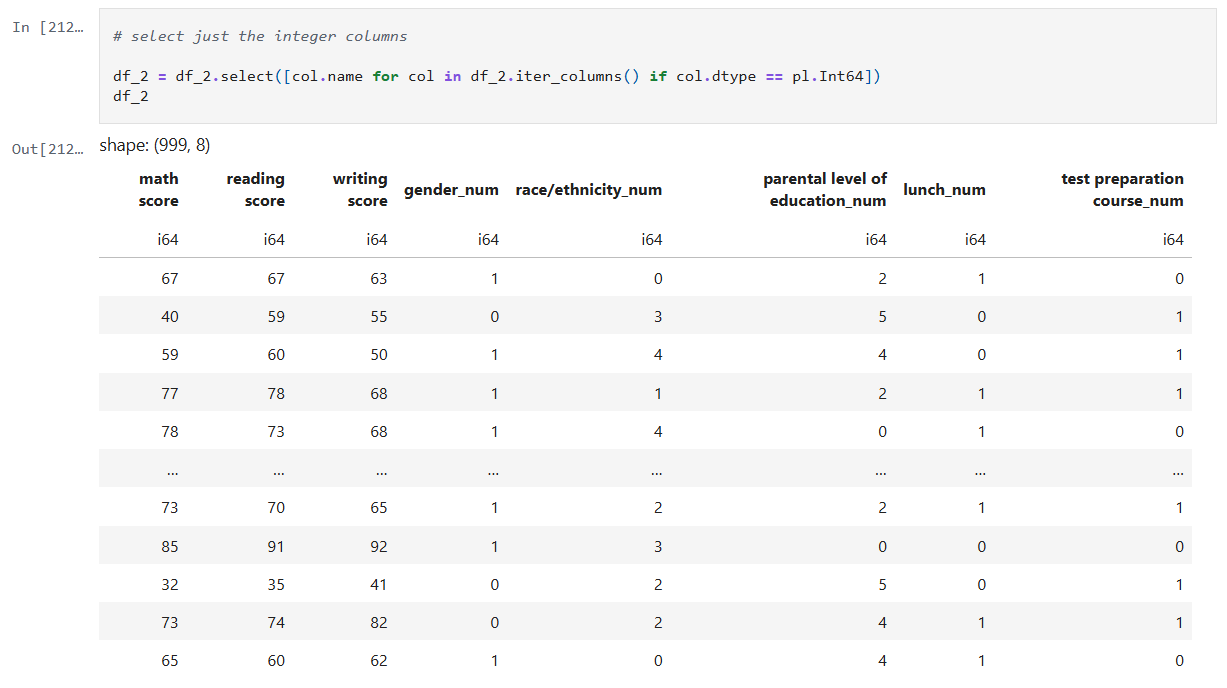
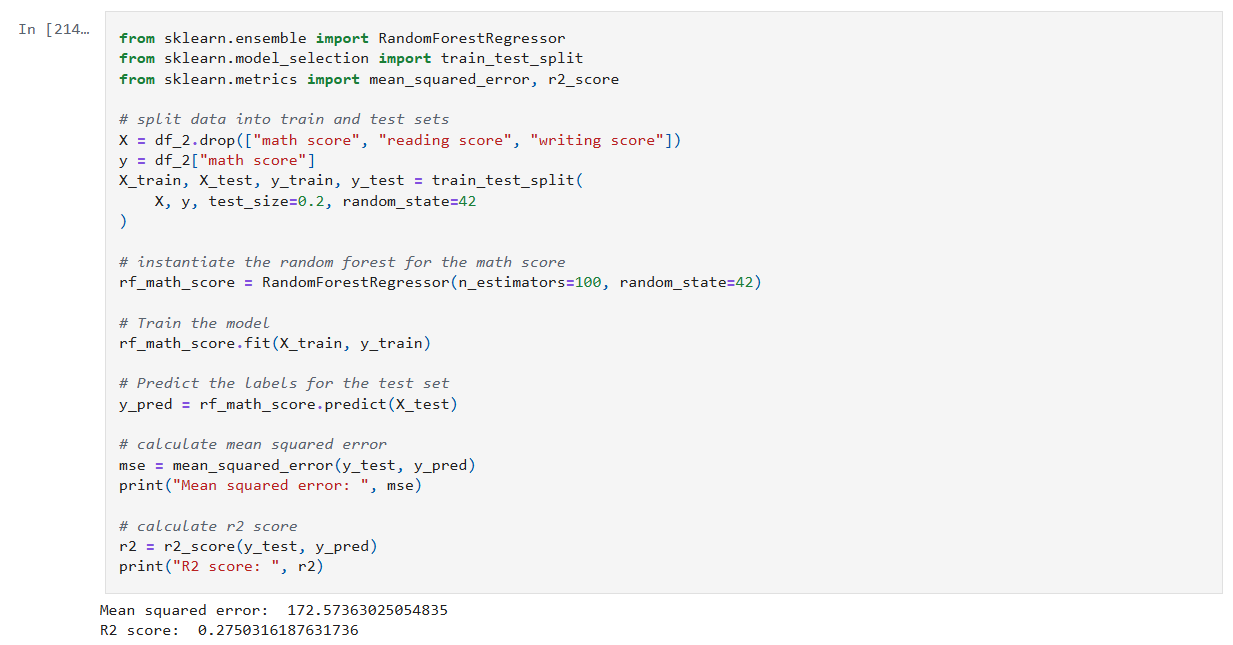
    In my previous post, I touched on model explainability. One approach for feature attribution is called SHAP, SHapley Additive exPlanations. In this post I will cover my first experiment with SHAP, building on one of my previous notebooks. My GitHub repo containing all of my Jupyter notebooks can be found here: GitHub – wcaubrey/learning-naive-bayes.

    What is SHAP

    SHAP (SHapley Additive Explanations) is a powerful technique for interpreting machine learning models by assigning each feature a contribution value toward a specific prediction. It’s grounded in Shapley values from cooperative game theory, which ensures that the explanations are fair, consistent, and additive.

    What SHAP Does

    • It calculates how much each feature “adds” or “subtracts” from the model’s baseline prediction.
    • It works both locally (for individual predictions) and globally (across the dataset).
    • It produces visualizations like force plots, summary plots, and dependence plots.

    What SHAP Is Good For

    • Trust-building: Stakeholders can see why a model made a decision.
    • Debugging: Helps identify spurious correlations or data leakage.
    • Fairness auditing: Reveals if certain features disproportionately affect predictions for specific groups.
    • Feature attribution: Quantifies the impact of each input on the output.

    Ideal Use Cases

    • Tree-based models (e.g., XGBoost, LightGBM, Random Forest)
    • High-stakes domains like healthcare, education, finance, and policy
    • Any scenario where transparency and accountability are critical

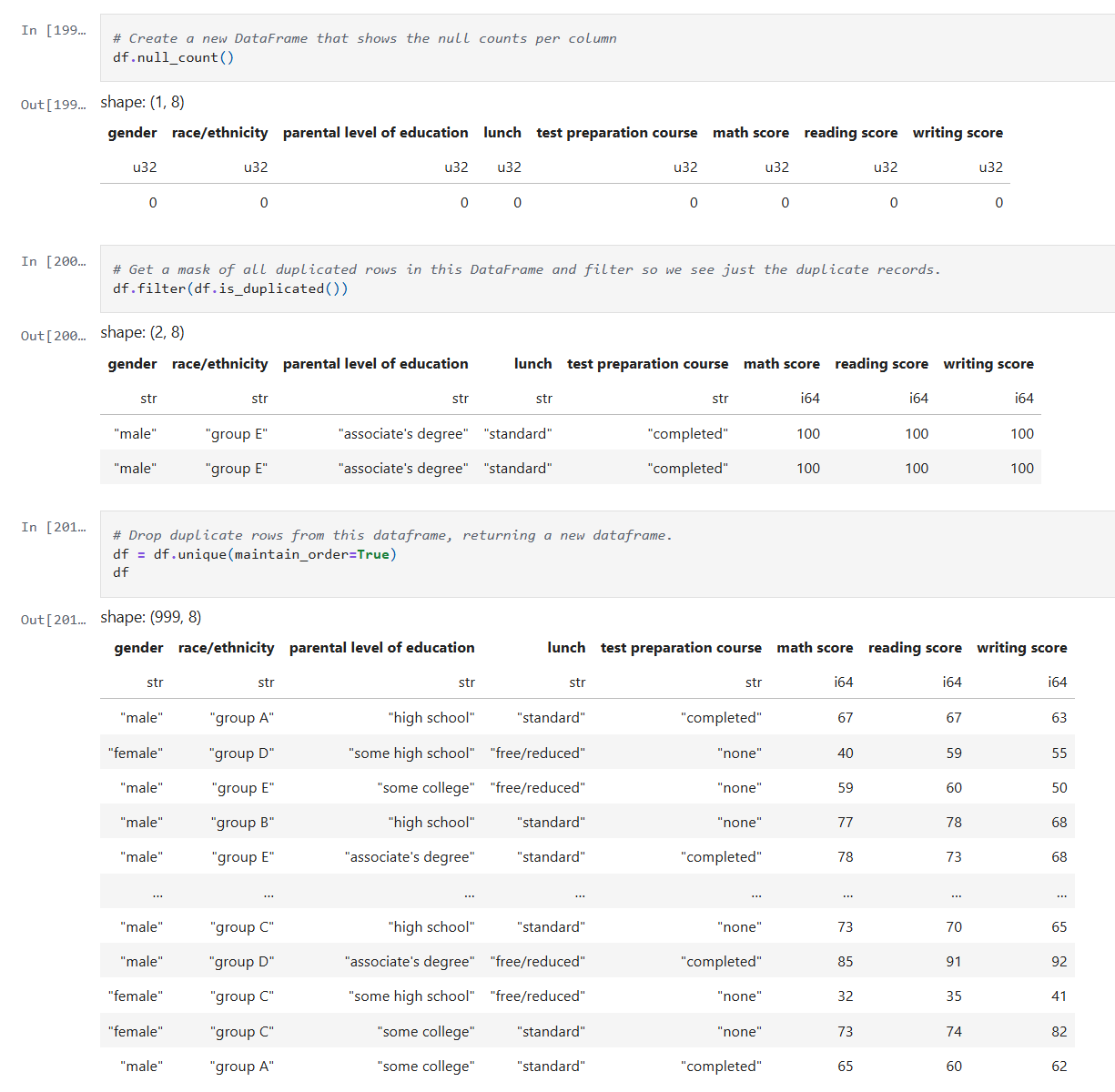
    My notebook changes

    In this new cell, I use the results of the previous grid search to create a SHAP TreeExplainer from the shap package. With that I create three different types of plots: a summary beeswarn, dependence and force plot.

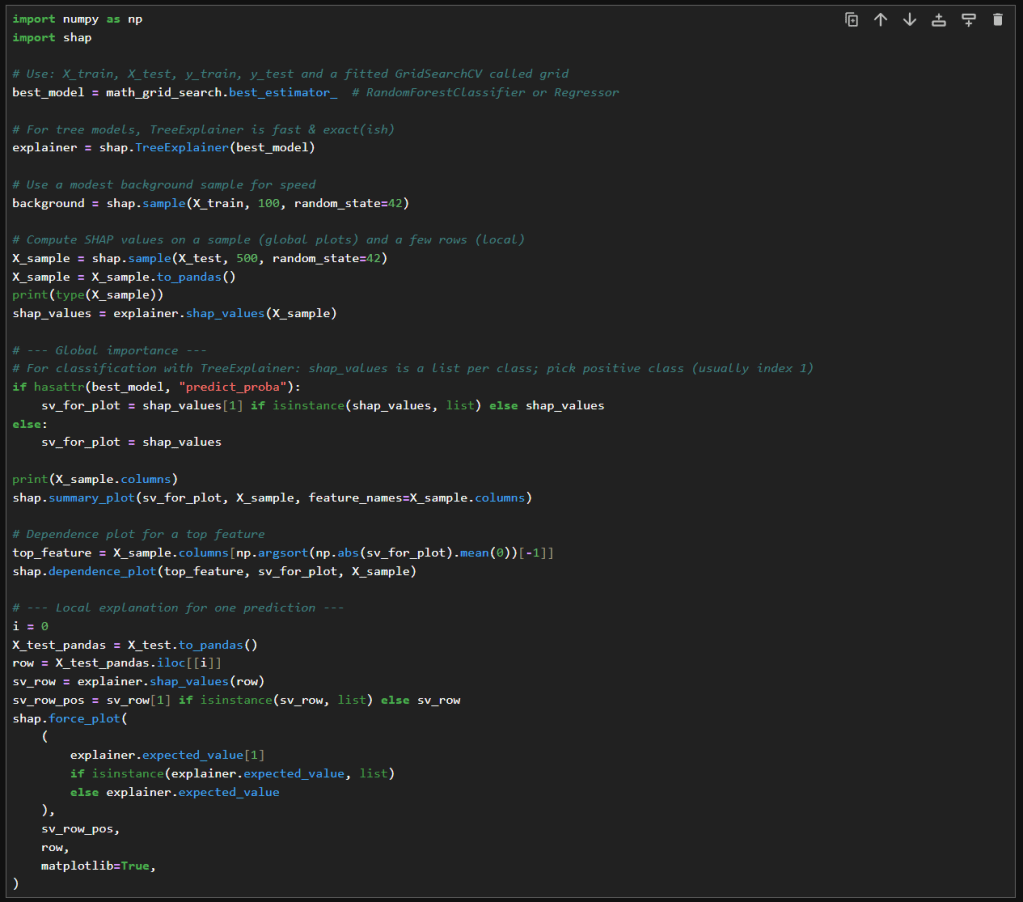
    SHAP Visualizations

    Interpreting the summary beeswarm plot

    The x-axis shows the SHAP values. Positive values push the prediction higher, towards the positive class or higher score. Negative values push the prediction lower.

    The y-axis shows the features, ranked by overall importance. The most important features are at the top. The spread of SHAP values shows how much influence that feature can have. The wider the spread of dots along the x-axis, the more variability that feature contributes to predictions. Narrow spreads mean the feature has a consistent, smaller effect.

    Each dot represents a single observation for the feature. The color of the dots shows the feature value. Red for high values and blue for low.

    If high feature values (red dots) cluster on the right (positive SHAP values), then higher values of that feature increase the prediction. If high values cluster on the left, then higher values decrease the prediction. Blue dots (low feature values) show the opposite effect.

    Overlapping colors can suggest interactions. For example, if both high and low values of a feature appear on both sides, the feature’s effect may depend on other variables.

    Interpreting the force plot

    The base value is the average model prediction if no features were considered. It’s like the starting point. It is the neutral prediction before considering any features.

    Arrows or bars are the force each feature contributes positively or negatively to the prediction. Each feature either increases or decreases the prediction. The size of the arrow/bar shows the magnitude of its effect.

    • Red (or rightward forces): Push the prediction higher.
    • Blue (or leftward forces): Push the prediction lower.

    The final prediction is the sum of the baseline plus all feature contributions. The endpoint shows the model’s actual output for that instance

    – William

    References

  • Making Sense of the Black Box: A Guide to Model Explainability

    Making Sense of the Black Box: A Guide to Model Explainability

    William's Data Science Blog

    In an age of AI-driven decisions, whether predicting student risk, approving loans, or diagnosing disease, understanding why a model makes a prediction is just as important as the prediction itself. This is exactly the purpose of model explainability.

    What Is Model Explainability?

    Model explainability refers to techniques that help us understand and interpret the decisions made by machine learning models. While simple models like linear regression are more easily interpretable, more powerful models, like random forests, gradient boosting, or neural networks, are often considered “black boxes”.

    Explainability tools aim to make it possible to understand that “box”, offering insights into how features influence predictions, both globally (across the dataset) and locally (for individual cases).

    Why It Matters: Trust, Transparency, and Actionability

    Explainability isn’t just a technical concern, it’s important for data scientists and society. Here’s why it matters:

    • Trust: Stakeholders are more likely to act on model outputs when they understand the reasoning behind them. A principal won’t intervene based on a risk score alone but will if they see that the score is driven by declining attendance and recent disciplinary actions.

    • Accountability: Explainability supports ethical AI by surfacing potential biases and enabling audits. It helps answer: “Is this model fair across different student groups?”

    • Debugging: Helps data scientists identify spurious correlations, data leakage, or overfitting.

    • Compliance: Increasingly required by regulations like GDPR (right to explanation), FERPA (student data protections), and the EU AI Act.

    Key Explainability Techniques

    Let’s explore and compare the most widely used methods:

    MethodTypeStrengthsLimitationsBest For
    SHAP (SHapley Additive Explanations)Local + GlobalTheoretically grounded, consistent, visual.Computationally expensive for large models.Tree-based models (e.g., XGBoost, RF).
    LIME (Local Interpretable Model-agnostic Explanations)LocalModel-agnostic, intuitive.Sensitive to perturbations, unstable explanations.Any black-box model.
    PDP (Partial Dependence Plot)GlobalShows marginal effect of features.Assumes feature independence.Interpreting average trends.
    ICE (Individual Conditional Expectation)LocalPersonalized insights.Harder to interpret at scale.Individual predictions.
    Permutation ImportanceGlobalSimple, model-agnostic.Can be misleading with correlated features.Quick feature ranking.

    SHAP vs. LIME: A Deeper Dive

    Both SHAP and LIME aim to answer the same question: “Why did the model make this prediction?” But they approach it from different angles, with distinct strengths, limitations, and implications for trust and usability.

    Theoretical Foundations

    AspectSHAPLIME
    Core IdeaBased on Shapley values from cooperative game theory.Builds a local surrogate model using disturbed samples.
    Mathematical GuaranteeAdditive feature attributions that sum to the model output.There is no guarantee of consistency or additivity.
    Model AssumptionsAssumes access to the model’s internal structure.Treats the model as a black box.
    • SHAP treats each feature as a “player” in a game contributing to the final prediction. It calculates the average contribution of each feature across all possible feature combinations.
    • LIME perturbs (disturbs) the input data around a specific instance and fits a simple interpretable model (usually linear) to approximate the local decision boundary.

    Output and Visualization

    FeatureSHAPLIME
    Local ExplanationForce plots show how each feature pushes the prediction.Bar charts show feature weights in the surrogate model.
    Global ExplanationSummary plots aggregate SHAP values across the dataset.Not designed for global insights.
    Visual IntuitionHighly visual and intuitive.Simpler but less expressive visuals.
    • SHAP’s force plots and summary plots are really great for stakeholder presentations. They show not just which features mattered, but how they interacted.
    • LIME’s bar charts are easier to generate and interpret quickly, but they can vary significantly depending on how the data was disturbed.

    Practical Considerations

    FactorSHAPLIME
    SpeedSlower, especially for large models.Faster, lightweight.
    StabilityHigh, same input yields same explanation.Low, results can vary across runs.
    Model SupportOptimized for tree-based models.Works with any model (including neural nets, ensembles!).
    ImplementationRequires more setup and compute.Easier to plug into existing workflows.
    • SHAP is ideal for production-grade models where consistency and auditability matter.
    • LIME is great for quick prototyping, debugging, or when working with opaque models like deep neural networks.

    A Real-World Example: Explaining Student Risk Scores

    My nonprofit’s goal is to build a model to identify students at risk of socio-emotional disengagement. The model uses features like attendance, GPA trends, disciplinary records, and survey responses.

    Let’s say the model flags a student as “high risk”. Without explainability, this is a black-box label. But with SHAP, we can generate a force plot that shows:

    • Attendance rate: -0.25 (low attendance strongly contributes to risk)
    • GPA change over time: -0.15 (declining grades add to concern)
    • Recent disciplinary action: +0.30 (a major driver of the risk score)
    • Survey response: “I feel disconnected from school”: +0.20 (adds emotional context)

    This breakdown transforms a numeric score into a narrative. It allows educators to:

    • Validate the prediction: “Yes, this aligns with what we’ve seen.”
    • Take targeted action: “Let’s prioritize counseling and academic support.”
    • Communicate transparently: “Here’s why we’re reaching out to this student.”

    Summary

    Model explainability isn’t just a technical add-on, it’s an ethical and operational imperative. As we build systems that influence real lives, we must ensure they are not only accurate but also understandable, fair, and trustworthy.

    – William

    References

    Technical Foundations of SHAP and LIME

  • Using Random Forests to analyze student performance

    Using Random Forests to analyze student performance

    William's Data Science Blog

    In this post, I’ll walk through my first notebook exploring random forests. I’m using a dataset I found on Kaggle. It can be found here: https://www.kaggle.com/datasets/whenamancodes/students-performance-in-exams/data.

    This is a small, simulated dataset that contains data for gender, ethnicity, the level of education attained by the parents, the lunch (free or standard), whether the student took test preparation courses and the scores for math, reading and writing.

    I’ll try my hand at using random forests to understand the importance of various features on student performance.

    Step 1: Clean up the data

    After reading the data into a Dataframe, we do a quick check on the quality of the data. I check for simple things like empty values and duplicates using Polars APIs.

    Below is the code from our notebook cell:

    In these cells:

    • Check for null data.
    • Check for duplicate rows and remove the duplicates.

    This makes sure we correct and, or remove any bad data before we start processing.

    Step 2: Inspect the data

    Now that the data is cleaned up, we can create some visualizations of the data. The first I’ll create are some histograms of the math, reading and writing scores. Histograms are one of the most foundational, and surprisingly powerful, visual tools in a data scientist’s toolkit.

    Below is the code from three notebook cells to generate the histograms:

    Histograms allow us to:

    • See whether the data is symmetrical or not.
    • See if there are a lot of outliers that could impact model performance.

    Next we’ll look at some boxplots. Boxplots are good for summarizing the distribution of the data.

    Boxplots allow us to visualize:

    • The median value of our features. The median represents the central tendency.
    • The interquartile range (IQR), showing the middle 50% of data.
    • The min and max values (excluding outliers).
    • Data outliers. Outliers are represented by the circles outside of 1.5 * the IQR.
    • Assess skewness. We can see of the median is very close to the top or bottom of the box.

    Next, we’ll look a heatmap. Heatmaps (or heatplots) are really powerful data visualizations, they let you see relationships between variables at a glance, especially when you’re dealing with large datasets or multiple features.

    Heatmaps allow us to visualize:

    • Correlations: Bright colors show strong positive or negative correlations while faded or neutral colors imply weak or no relationship.
    • Spotting Patterns: We can quickly identify where performance clusters, or drops, occur.
    • Identifying Anomalies: Visual blips can point to data quality problems.

    Step 3: Encoding Categorical Variables

    The next step is to convert our categorical columns to a numeric format using scikit-learn’s LabelEncoder.

    Below is the code from our notebook cell:

    In that cell:

    • I instantiate a LabelEncoder object.
    • I get the names of the columns that need to be encoded by iterating over the columns in the dataframe and filtering where the type of the column is a string.
    • I create encoded data for each of those columns with a new name appended with “_num”.
    • Lastly I create a new dataframe that combines the new columns I created with the original dataframe.

    Step 4: Remove the non-numeric columns

    This is a simple step, where I simply select the columns that are integers.

    Below is the code from our notebook cell:

    In that cell:

    • Iterate over the columns, filtering where the type is integer and use that list in the select function.

    Now we can create a heatmap that includes the encoded data too.

    Step 5: Train models for math, reading and writing

    Now it’s time to build, train, and evaluate our model. I repeat this step for each of the math, reading and writing scores. I’ll only show the math cell here as they do the same thing.

    In that cell:

    • Drop the score columns from the dataframe.
    • Choose “math score” as my category column.
    • Split the data and create a RandomForestRegressor model.
    • Train the model against the data.
    • Use the model to predict values and measure the accuracy.

    The r2 score gives a sense of how well the predictors capture the ups-and-downs in your target. Or: How much better is my model at predicting Y than just guessing the average of Y every time?

    • R² = 1: indicates a perfect fit.
    • R² = 0: the model is no better than predicting the mean.
    • R² < 0: the model is worse than the mean.

    Step 6: Visualize feature importance to the math score

    Now we can create a histogram to visualize the relative importance of our features to the math score.

    In that cell:

    • I grab all the feature columns.
    • Map the columns to the models feature_importances_ value.
    • Generate a plot.
    The higher the value in feature_importances_, the more important the feature.

      Final Thoughts and Next Steps

      In this first step into learning about Random Forests we can see they are powerhouse in the world of data science. Random Forests are built on the idea of “wisdom of the crowd”, by combining many decision trees trained on random subsets of data and features, they reduce overfitting and improve generalization.

      The new Jupyter notebook can be found here in my GitHub.

      – William

    • Deep Dive Into Random Forests

      Deep Dive Into Random Forests

      William's Data Science Blog

      In today’s post, I’ll take an in-depth look at Random Forests, one of the most popular and effective algorithms in the data science toolkit. I’ll describe what I learned about how they work, their components and what makes them tick.

      What Are Random Forests?

      At its heart, a random forest is an ensemble of decision trees working together.

      • Decision Trees: Each tree as a model that makes decisions by splitting data based on certain features.
      • Ensemble Approach: Instead of relying on a single decision tree, a random forest builds many trees from bootstrapped samples of your data. The prediction from the forest is then derived by averaging (for regression) or taking a majority vote (for classification).

      This approach reduces the variance typical of individual trees and builds a robust model that handles complex feature interactions with ease.

      The Magic Behind the Method

      1. Bootstrap Sampling

      Each tree in the forest is trained on a different subset of data, selected with replacement. This process, known as bagging (Bootstrap Aggregating), means roughly 37% of your data isn’t used in any tree. This leftover data, the out-of-bag (OOB) set, can later be used to internally validate the model without needing a separate validation set.

      2. Random Feature Selection

      At every decision point within a tree, instead of considering every feature, the algorithm randomly selects a subset. This randomness:

      • De-correlates Trees: Each tree becomes less alike, ensuring that the ensemble doesn’t overfit or lean too heavily on one feature.
      • Reduces Variance: Averaging predictions across diverse trees smooths out misclassifications or prediction errors.

      3. Aggregating Predictions

      For classification tasks, each tree casts a vote for a class, and the class with the highest number of votes becomes the model’s prediction.

      For regression tasks, predictions are averaged to produce a final value. This collective approach generally results in higher accuracy and more stable predictions.

      Out-of-Bag (OOB) Error

      An important feature of random forests is the OOB error estimate.

      • What It Is: Each tree is trained on a bootstrap sample, leaving out a set of data that can serve as a mini-test set.
      • Why It Counts: Aggregating predictions on these out-of-bag samples can offer an estimate of the model’s test error.

      This feature can be really handy, especially when you’re working with limited data and want to avoid setting aside a large chunk of it for validation.

      Feature Importance

      Random forests don’t just predict, they can also help you understand your data:

      • Mean Decrease in Impurity (MDI): This measure tallies how much each feature decreases impurity (based on measures like the Gini index) across all trees.
      • Permutation Importance: By shuffling features and measuring the drop in accuracy the importance of a feature can be measured. This is meant to help when you need to interpret the model and communicate which features are most influential.

      Pros and Cons

      Advantages:

      • Can handle Non-Linear Data: Naturally captures complex feature interactions.
      • Can handle Noise & Outliers: Ensemble averaging minimizes overfitting.
      • Doesn’t need a lot of Preprocessing: No need for extensive data scaling or transformation.

      Disadvantages:

      • Can be Memory Intensive: Storing hundreds of trees can be demanding.
      • Slower than a single Tree: Compared to a single decision tree, the ensemble approach require more processing power.
      • Harder to Interpret: The combination of multiple trees makes it harder to interpretability compared to individual trees.

      Summary

      Random Forests are a powerful next step in my journey. With their ability to reduce variance through ensemble learning and their built-in validation mechanisms like OOB error, they offer both performance and insight.

      In my next post, I’ll share how I apply the Random Forest technique to this data set: https://www.kaggle.com/datasets/whenamancodes/students-performance-in-exams/data

      – William