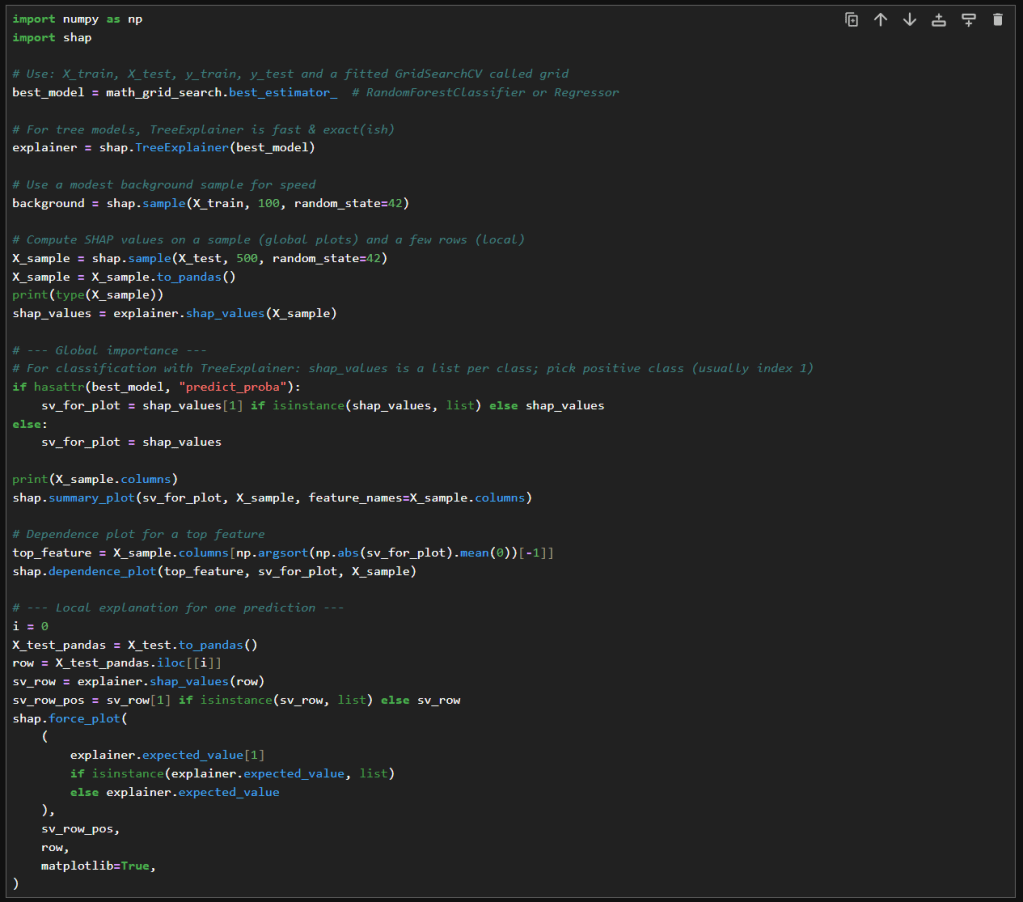
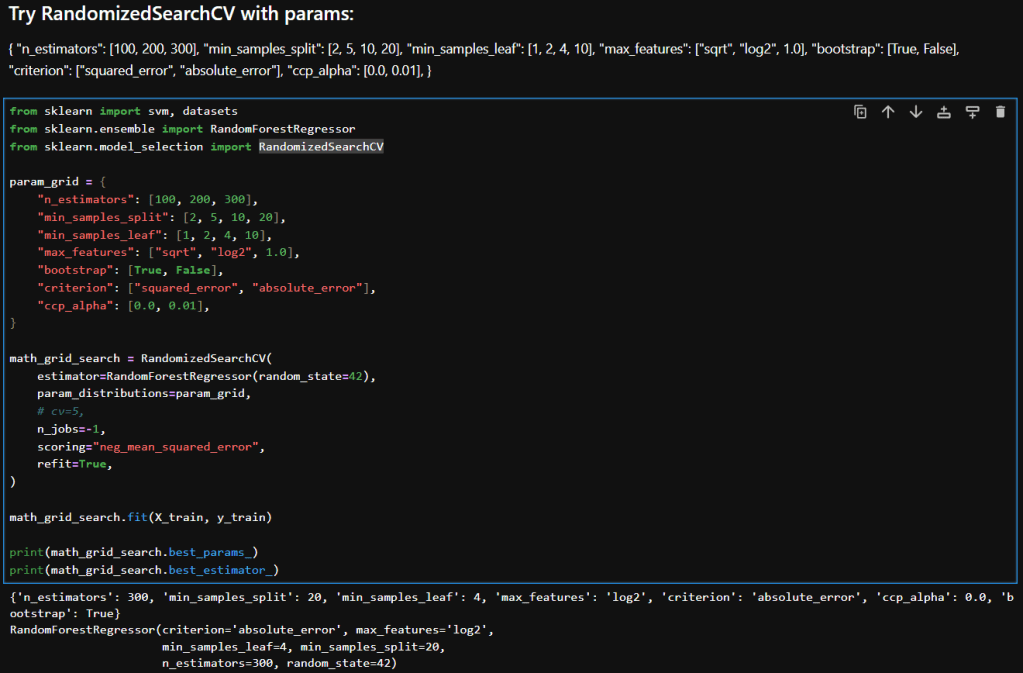
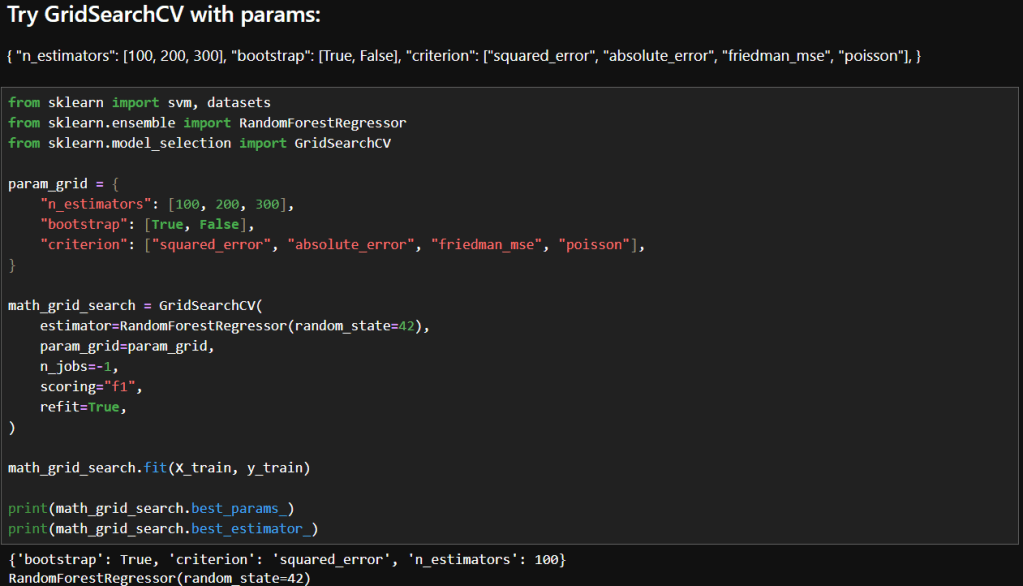
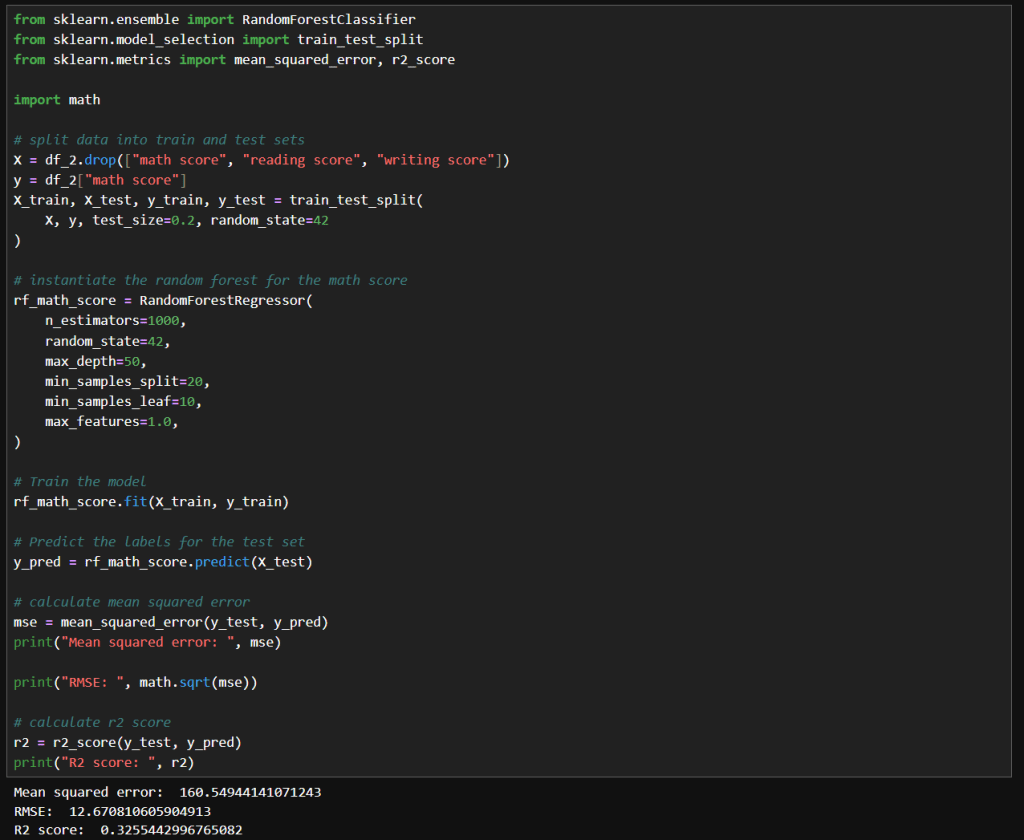
I owe you an apology. I disappeared for a bit because I was trapped in the ninth circle of the college‑application process, otherwise known as “writing essays.” So many essays. I needed a rest! But I’ve resurfaced, slightly overcaffeinated and definitely overshared, and I’m ready to talk about something far more relaxing than applications: evolutionary computation.
I stumbled across this branch of data science and found it so cool I started reading more and wanted to share what I found. Evolutionary computation is cool because it feels like the closest thing computer science has to science fiction. It is one of the rare techniques where the machine genuinely surprises you because it’s creative in a way that mirrors nature itself.
When Algorithms Evolve: The Story of Genetic Algorithms
There is something so cool about the idea that algorithms can evolve. Not in the metaphorical sense, but in the literal, biological sense, where solutions compete, adapt, and survive the same way living things do. It’s a reminder that not everything has to follow a straight line.
Genetic algorithms grew out of that spirit of curiosity. They offered a way to explore problems that were too messy or too unpredictable for traditional methods. For a while, they captured the imagination of researchers, engineers, and artists, because they made computation feel creative. Even today, long past their time in the spotlight, they still have a strange and enduring charm.
What Genetic Algorithms Actually Do
Genetic algorithms search for solutions by treating them like organisms in a population. Each candidate competes, reproduces, and mutates, and over generations the population evolves to a solution. They explore, stumble, adapt, and occasionally discover solutions no human would have thought to try.
This makes them especially useful in problems where intuition fails and the search space complex.
A Brief History
As I mentioned, genetic algorithms emerged in the 1960s through the work of John Holland at the University of Michigan. His research asked a completely new question. If evolution can produce complex organisms without a designer, could computation do the same?
By the 1980s and 1990s, this idea had spread far beyond academia. Engineers at NASA once used a genetic algorithm to design an antenna for a spacecraft. They fed the system a set of constraints, pressed go, and watched as each generation twisted itself into stranger shapes. The final design looked like a bent paperclip someone had stepped on, but it outperformed every hand‑crafted alternative.
In architecture studios, designers sometimes let genetic algorithms “grow” building facades. The results look like coral reefs or alien cathedrals, and half the fun is seeing what the algorithm thinks is beautiful.
At that time in computing history, genetic algorithms were more than tools. They were a philosophy. They suggested that creativity could be computational and exploration could be automated.
Why Genetic Algorithms Were So Beloved
They could function in messy data. If you had a problem where the objective function was noisy, discontinuous, or simply weird, a genetic algorithm didn’t care.
They were very flexible. You could encode almost anything, from bits to rules or even a neural network architecture, and evolution would happily go to work. This flexibility made it feel like they could solve any optimization problem.
They were also intuitive. People already understood evolution. The user didn’t need to understand calculus to understand how genetic algorithms work. That made them an entry point into computational thinking for many students and researchers.
What I love about genetic algorithms is that they take something that is too complicated to understand all at once, start wide, stay curious, and only narrow in when the evidence earns it. That feels very relevant outside of computation.
Curiosity on its own doesn’t guarantee efficiency. As the field grew, machine learning shifted toward methods that rewarded precision over exploration.
Why Genetic Algorithms Faded from the Spotlight
As machine learning matured, new methods emerged that were faster, more efficient, and more predictable. For example, Bayesian optimization offered a smarter way to search with fewer evaluations.
In many areas of data science, genetic algorithms couldn’t compete with the speed and precision of newer techniques. Genetic algorithms were powerful generalists in a world that increasingly rewarded specialists. Their strengths did not disappear; they just became less central as the field evolved.
Where Genetic Algorithms Still Shine
Today, genetic algorithms still thrive in places where the search space is too messy for calculus and too highly dimensional for brute force.
In engineering, genetic algorithms are still used to design structures that must balance competing constraints such as strength, weight, cost, and manufacturability. These are problems with no clean analytic path. In robotics, evolutionary strategies help discover control policies that are robust in the face of noise and uncertainty. In creative fields, genetic algorithms still generate art, music, and architectural forms.
Even in machine learning, they have not disappeared. Genetic algorithms are used for feature selection when the relationships are too tangled. They are used to evolve neural network architectures in ways that other techniques cannot.
Genetic algorithms survive because they explore. Exploration is still necessary. In messy, unpredictable environments, exploration isn’t a luxury. It’s how systems can stay resilient.
A Reflection Through the Lens of the Early Signal Project
The Early Signal Project does not use genetic algorithms directly, but the philosophy behind them resonates deeply with the work.
Genetic algorithms show us that diversity is not noise. It is information. Populations thrive when they contain many possibilities, not when they are homogenous. Premature convergence is risky because it shuts down other possibilities. Exploration needs to come before optimization. Good solutions emerge through iteration, not assumption.
Early detection in education requires the same mindset. The goal isn’t to force everything into a single pattern. It’s to let patterns emerge honestly, even if they surprise you.
You should not rush to conclusions about a student based on a single signal. You need to explore patterns without prejudice. Let insights emerge from the data. Refine carefully, ethically, and with humility. Protect the diversity of student experiences rather than trying to force them into one narrative.
In that sense, the Early Signal Project is its own evolutionary system. It evolves toward clarity, fairness, and early support for students.
Closing Thoughts
Genetic algorithms remind us that progress can often come from embracing variation rather than suppressing it. They show that creativity can be computational, that exploration is as important as optimization, and that surprising solutions often emerge from processes we do not control.
In data science and in education, solutions evolve when we give room to breathe and adapt.
Sometimes the most powerful ideas are not the newest ones. They are the ones that remind us how to think and remind us how to stay curious.
– William