William's Data Science Blog

Tag: machine-learning

  • Playing with Hyperparameter Tuning and Winsorizing

    Playing with Hyperparameter Tuning and Winsorizing

    William's Data Science Blog

    In this post, I’ll revisit my earlier model’s performance by experimenting with hyperparameter tuning, pushing beyond default configurations to extract deeper predictive power. I’ll also take a critical look at the data itself, exploring how winsorizing outliers can recalibrate outliers without sacrificing the integrity of the data. The goal: refine, rebalance, and rethink accuracy.

    Hyperparameter Tuning

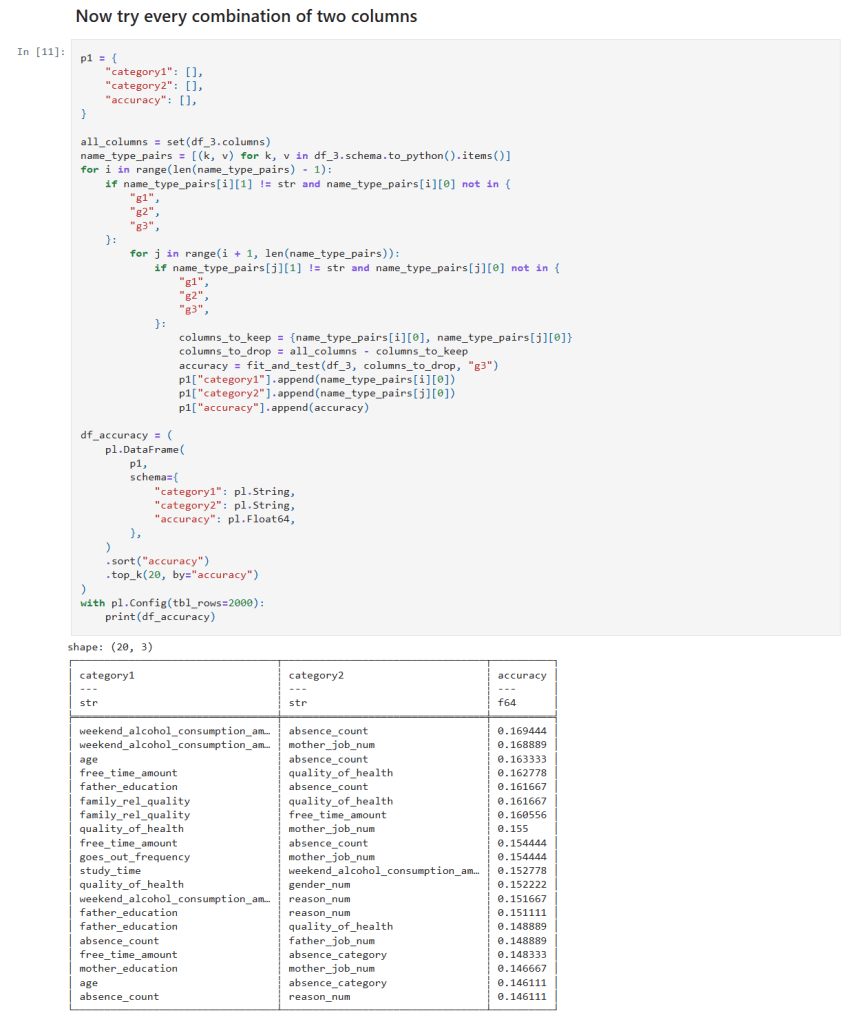
    The image below shows my initial experiment with the RandomForestRegressor. As you can see, I used the default value for n_estimators.

    The resulting MSE, RMSE and R² score are shown. In my earlier post I noted what those values mean. In summary:

    • An MSE of 172 indicates there may be outliers.
    • An RMSE of 13 indicates there an average error of around 13 points on 0–100 scale.
    • An R² of 0.275 means my model explains just 27.5% of the variance in the target variable.

    Experimentation

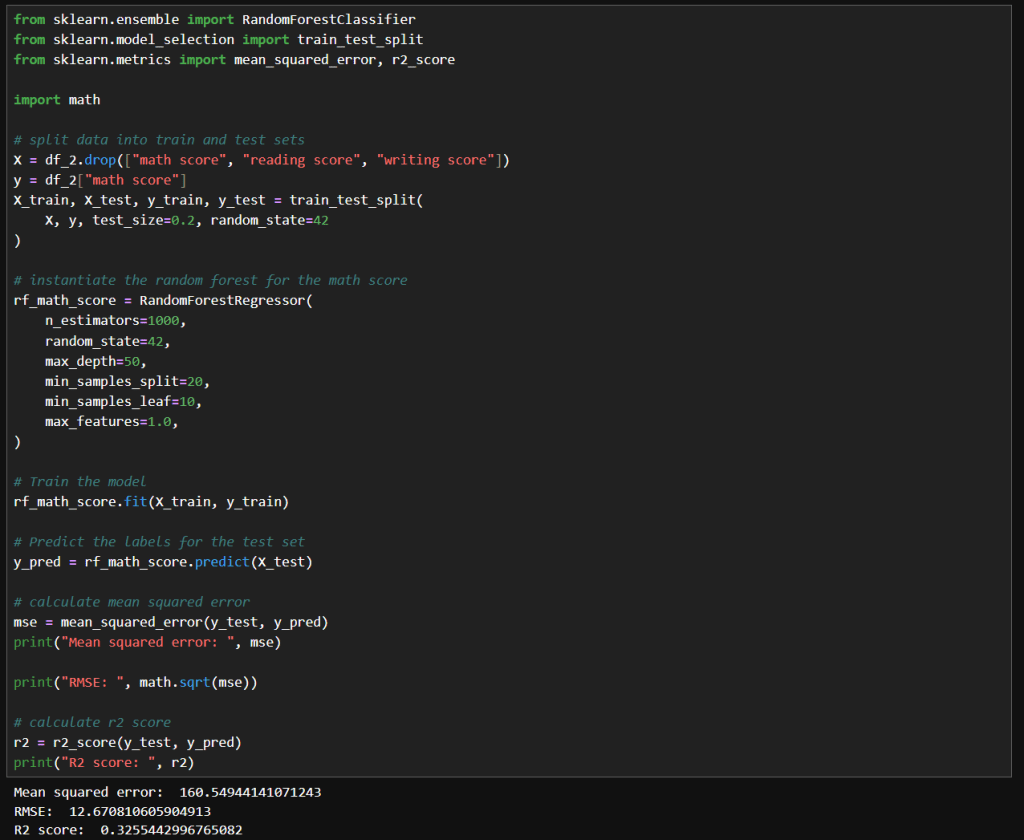
    My first attempt at manual tuning looked like the image below. There really is just a small improvement with these parameters. I tried increasing n_estimators significantly because the accuracy should be improved with the larger value. I tried increasing max_depth to 50 to see if that compares to the default value of None. I tried increasing min_samples_split to 20 and min_samples_leaf of 10 to see if it would help with any noise in the data. I didn’t really need to set max_features to 1.0, because that is currently the default value.

    The net result was slightly better results, but nothing too significant.

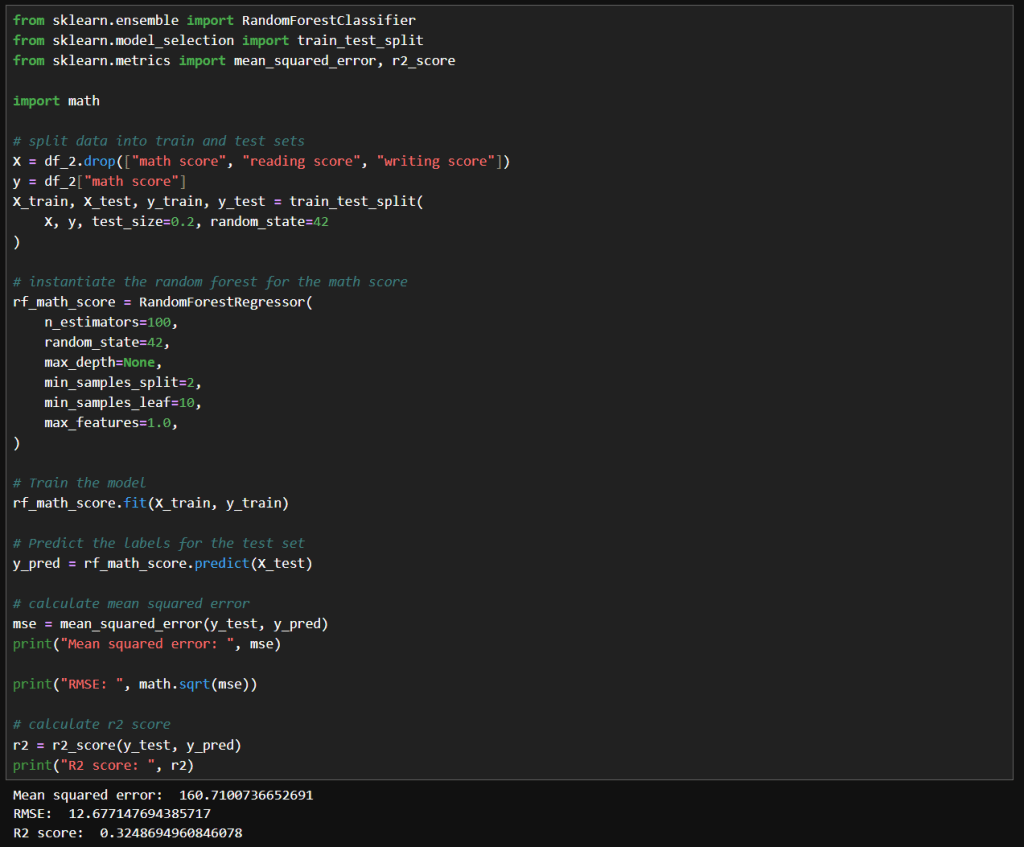
    Next, I tried what is shown in the image below. Interestingly, I got very similar results to the above. With these values, the model trains much faster while achieving the same results.

    Winsorizing

    Winsorization changes a dataset by replacing outlier values with less extreme ones. Unlike trimming (which removes outliers), winsorization preserves the dataset size by limiting values at the chosen threshold.

    Here is what my code looks like:

    In this cell, I’ve replaced the math score data a winsorized version. I used the same hyperparameters as before. Here we can see a more significant improvement MSE and RMSE, but a slightly lower R² score.

    That means that since the earlier model has a slightly higher R², it explains a bit more variance relative to the total variance of the target variable. Maybe because it models the core signal more tightly, even though it has noisier estimates.

    The winsorized model, with its lower MSE and RMSE indicate better overall prediction accuracy. This is nice when minimizing absolute error matters the most.

    Final Thoughts

    After experimenting with default settings, I systematically adjusted hyperparameters and applied winsorization to improve my RandomForestRegressor’s accuracy. Here’s a concise overview of the three main runs:

    • Deep, Wide Forest
      • Parameters
        • max_depth: 50
        • min_samples_split: 20
        • min_samples_leaf: 10
        • max_features: 1.0
        • random_state: 42
      • Insights
        • A large ensemble with controlled tree depth and higher split/leaf thresholds slightly reduced variance but yielded only marginal gains over defaults.
    • Standard Forest with Unlimited Depth
      • Parameters
        • max_depth: None
        • min_samples_split: 2
        • min_samples_leaf: 10
        • max_features: 1.0
        • random_state: 42
      • Insights
        • Reverting to fewer trees and no depth limit produced nearly identical performance, suggesting diminishing returns from deeper or wider forests in this setting.
    • Winsorized Data
      • Parameters
        • n_estimators: 100
        • max_depth: None
        • min_samples_split: 2
        • min_samples_leaf: 10
        • max_features: 1.0
        • random_state: 42
        • Applied winsorization to cap outliers
      • Insights
        • Winsorizing outliers drastically lowered absolute error (MSE/RMSE), highlighting its power for stabilizing predictions. The slight drop in R² reflects reduced target variance after capping extremes.

    – William

  • Deep Dive Into Random Forests

    Deep Dive Into Random Forests

    William's Data Science Blog

    In today’s post, I’ll take an in-depth look at Random Forests, one of the most popular and effective algorithms in the data science toolkit. I’ll describe what I learned about how they work, their components and what makes them tick.

    What Are Random Forests?

    At its heart, a random forest is an ensemble of decision trees working together.

    • Decision Trees: Each tree as a model that makes decisions by splitting data based on certain features.
    • Ensemble Approach: Instead of relying on a single decision tree, a random forest builds many trees from bootstrapped samples of your data. The prediction from the forest is then derived by averaging (for regression) or taking a majority vote (for classification).

    This approach reduces the variance typical of individual trees and builds a robust model that handles complex feature interactions with ease.

    The Magic Behind the Method

    1. Bootstrap Sampling

    Each tree in the forest is trained on a different subset of data, selected with replacement. This process, known as bagging (Bootstrap Aggregating), means roughly 37% of your data isn’t used in any tree. This leftover data, the out-of-bag (OOB) set, can later be used to internally validate the model without needing a separate validation set.

    2. Random Feature Selection

    At every decision point within a tree, instead of considering every feature, the algorithm randomly selects a subset. This randomness:

    • De-correlates Trees: Each tree becomes less alike, ensuring that the ensemble doesn’t overfit or lean too heavily on one feature.
    • Reduces Variance: Averaging predictions across diverse trees smooths out misclassifications or prediction errors.

    3. Aggregating Predictions

    For classification tasks, each tree casts a vote for a class, and the class with the highest number of votes becomes the model’s prediction.

    For regression tasks, predictions are averaged to produce a final value. This collective approach generally results in higher accuracy and more stable predictions.

    Out-of-Bag (OOB) Error

    An important feature of random forests is the OOB error estimate.

    • What It Is: Each tree is trained on a bootstrap sample, leaving out a set of data that can serve as a mini-test set.
    • Why It Counts: Aggregating predictions on these out-of-bag samples can offer an estimate of the model’s test error.

    This feature can be really handy, especially when you’re working with limited data and want to avoid setting aside a large chunk of it for validation.

    Feature Importance

    Random forests don’t just predict, they can also help you understand your data:

    • Mean Decrease in Impurity (MDI): This measure tallies how much each feature decreases impurity (based on measures like the Gini index) across all trees.
    • Permutation Importance: By shuffling features and measuring the drop in accuracy the importance of a feature can be measured. This is meant to help when you need to interpret the model and communicate which features are most influential.

    Pros and Cons

    Advantages:

    • Can handle Non-Linear Data: Naturally captures complex feature interactions.
    • Can handle Noise & Outliers: Ensemble averaging minimizes overfitting.
    • Doesn’t need a lot of Preprocessing: No need for extensive data scaling or transformation.

    Disadvantages:

    • Can be Memory Intensive: Storing hundreds of trees can be demanding.
    • Slower than a single Tree: Compared to a single decision tree, the ensemble approach require more processing power.
    • Harder to Interpret: The combination of multiple trees makes it harder to interpretability compared to individual trees.

    Summary

    Random Forests are a powerful next step in my journey. With their ability to reduce variance through ensemble learning and their built-in validation mechanisms like OOB error, they offer both performance and insight.

    In my next post, I’ll share how I apply the Random Forest technique to this data set: https://www.kaggle.com/datasets/whenamancodes/students-performance-in-exams/data

    – William

  • Exploring the Impact of Alcohol Consumption on Student Grades with Gaussian Naive Bayes

    Exploring the Impact of Alcohol Consumption on Student Grades with Gaussian Naive Bayes

    William's Data Science Blog

    In today’s data-driven world, even seemingly straightforward questions can reveal surprising insights. In this post, I investigate whether students’ alcohol consumption habits bear any relationship to their final math grades. Using the Student Alcohol Consumption dataset from Kaggle, which contains survey responses on a myriad aspects of students’ lives—ranging from study habits and social factors to gender and alcohol use—I set out to determine if patterns exist that can predict academic performance.

    Dataset Overview

    The dataset originates from a survey of students enrolled in secondary school math and Portuguese courses. It includes rich, social, and academic information, such as:

    • Social and family background
    • Study habits and academic support
    • Alcohol consumption details during weekdays and weekends

    I focused on predicting the final math grade (denoted as G3 in the raw data) while probing how alcohol-related features, especially weekend consumption, might play a role in performance. The binary insight wasn’t just about whether students drank, but which drinking pattern might be more telling of their academic results.

    Data Preprocessing: Laying the Groundwork

    Before diving into modeling, the data needed some cleanup. Here’s how I systematically prepared the dataset for analysis:

    1. Loading the Data: I imported the CSV into a Pandas DataFrame for easy manipulation.
    2. Renaming Columns: Clarity matters. I renamed ambiguous columns for better readability (e.g., renaming walc to weekend_alcohol and dalc to weekday_alcohol).
    3. Label Encoding: Categorical data were converted to numeric representations using scikit-learn’s LabelEncoder, ensuring all features could be numerically processed.
    4. Reusable Code: I encapsulated the training and testing phases within a reusable function, which made it straightforward to test different feature combinations.

    Here’s are some snippets:

    In those cells:

    • I rename columns to make them more readable.
    • I instantiate a LabelEncoder object and encode a list of columns that have string values.
    • I add an absence category to normalize absence count a little due to how variable that data is.

    Experimenting With Gaussian Naive Bayes

    The heart of this exploration was to see how well a Gaussian Naive Bayes classifier could predict the final math grade based on different selections of features. Naive Bayes, while greatly valued for its simplicity and speed, operates under the assumption that features are independent—a condition that might not fully hold in educational data.

    Training and Evaluation Function

    To streamline the experiments, I wrote a function that:

    • Splits the data into training and testing sets.
    • Trains a GaussianNB model.
    • Evaluates accuracy on the test set.

    In that cell:

    • I create a function that:
      • Drops unwanted columns.
      • Runs 100 training cycles with the given data.
      • Captures the accuracy measured from each run and returns the average.

    Single and Two column sampling

    In those cells:

    • I get a list of all columns.
    • I create loop(s) over the column list and create a list of features to test.
    • I call my function to measure the the accuracy of the features at predicting student grades.

    Diving Into Feature Combinations

    I aimed to assess the predictive power by testing different combinations of features:

    1. All Columns: This gave the best accuracy of around 22%, yet it was clear that even the full spectrum of information struggled to make strong predictions.
    2. Handpicked Features: I manually selected features that I hypothesized might be influential. The resulting accuracy dipped below that of the full dataset.
    3. Individual Features: Evaluating each feature solo revealed that the column indicating whether students planned to pursue higher education yielded the highest individual accuracy—though still far lower than all features combined.
    4. Two-Feature Combinations: By testing all pairs, I noticed that combinations including weekend alcohol consumption appeared in the top 20 predictive pairs four times, including in both of the top two.
    5. Three-Feature Combinations: The trend became stronger—combinations featuring weekend alcohol consumption topped the list ten times and were present in each of the top three combinations!
    6. Four-Feature Combinations: Here, weekend alcohol consumption featured in the top 20 combination results even more robustly—15 times in total.

    These experiments showcased one noteworthy pattern: weekend alcohol consumption consistently emerged as a common denominator in the best-performing feature combinations, while weekday consumption rarely made an appearance.

    Analysis of the Findings

    Several key observations emerged from this series of experiments:

    • Predictive Accuracy: Even with the full set of features, the best accuracy reached was only around 22%. This underwhelming performance is indicative of the challenges posed by the dataset and the restrictive assumptions embedded within the Naive Bayes model.
    • Role of Alcohol Consumption: The repeated appearance of weekend alcohol consumption in high-ranking feature combinations suggests a potential association—it may capture lifestyle or social habits that indirectly correlate with academic performance. However, it is not a standalone predictor; rather, it seems to be relevant as part of a multifactorial interaction.
    • Model Limitations: The Gaussian Naive Bayes classifier assumes feature independence. The complexities inherent in student performance—where multiple social, educational, and psychological factors interact—likely violate this assumption, leading to lower predictive performance.

    Conclusion and Future Directions

    While the Gaussian Naive Bayes classifier provided some interesting insights, especially regarding the recurring presence of weekend alcohol consumption in influential feature combinations, its overall accuracy was modest. Predicting the final math grade, a multifaceted outcome influenced by numerous interdependent factors, appears too challenging for this simplistic probabilistic model.

    Next Steps:

    • Alternative Machine Learning Algorithms: Investigating other approaches like decision trees, random forests, support vector machines, or ensemble methods may yield better performance.
    • Enhanced Feature Engineering: Incorporating interaction terms or domain-specific features might help capture the complex relationships between social habits and academic outcomes.
    • Broader Data Explorations: Diving deeper into other factors—such as study habits, parental support, and extracurricular involvement—could provide additional clarity.

    Final Thoughts and Next Steps

    This journey reinforced the idea that while Naive Bayes is a great tool for its speed and interpretability, it might not be the best choice for all datasets. More sophisticated models and careful feature engineering are necessary when dealing with some datasets like student academic performance.

    The new Jupyter notebook can be found here in my GitHub.

    – William